Sociopath Community

So with asymptotes, is that where elliptical curves come in?

Buttered Toast said: 

So with asymptotes, is that where elliptical curves come in?

The elliptical curves have more to do with how an algebraic structure can be imposed on a geometric one.

The mathematical object and its operations that comes from that then relates to primality and the properties of primes.

Modulo Arithmetic and some Algebra

This section will feel a little more abstract, so just bare with me because it will make more sense once the sections on Cryptography and Elliptic Curves are reached.

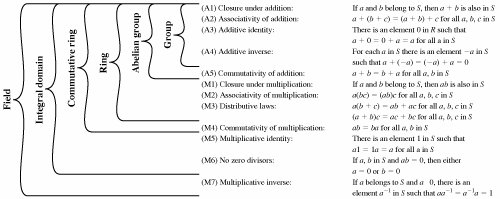
Group
A group is a set with a binary operation (+, .) and the following properties:
     (1) Identity,
           (1a) Under addition (+), 0 + a = a + 0 = a
           (1b) Under multiplication (.), 1.a = a.1 = a
    (2) Inverses,
           (2a) Under addition (+), a + (-a) = (-a) + a = 0
           (2b) Under multiplication (.), a.a^-1 = a^-1.a = 1
    (3) Associative,
           (3a) Under addition (+), a + (b + c) = (a + b) + c

           (3b) Under multiplication (.), a(bc) = (ab)c

Abelian Group
A group such that commutativity holds under the binary operation,
      Under addition, a + b = b + a
      Under multiplication, ab = ba

Ring
A ring R is a set with binary operations + and x with elements 0, 1 elements of R such that R is an abelian group under +, and for all a,b,c in R the follow properties hold:
     (1) Identity, 1a = a1 = a
     (2) Associativity, (ab)c = a(bc)
     (3) Distributivity, a(b + c) = ab + ac

A commutative ring will also have the commutative property for its binary operations.

Field
A field K is a ring such that for every nonzero element a in K there is an element b in K such that ab = 1

That is a field is a ring with the additional property of containing inverses for binary operators.

All of the above definitions are giving names to mathematical structures than any one who has taken algebra in HS has experience with.

The structures are determined by what kind of arithmetic makes sense given a set of mathematical objects like numbers,

a congruent to b modulo n
Given n in N and a,b in Z we say that a is congruent to b modulo n, written a ≅ b (mod n), if n|a - b

That is, nc = a - b where c in Z which implies c = (a-b)/n

Example.8 ≅ 3 (mod 5)
-> 5 | 8 - 3 -> 5(1) = 5 -> 5 = 5/1
20 ≅ 4 (mod 8)
-> 8 | 20 - 4 -> 8(2) = 16 -> 16/8 = 2

Integers Modulo n
The ring Z/nZ of integers modulo n is the set of equivalency classes of integers modulo n, written as [x] = {a in Z | a ≅ x (mod n)}.

Example. let n = 5 with varying x, that is Z/5Z
[0] = {. . ., -5, 0, 5, . . .} = 0 + 5z
[1] = {. . ., -4, 1, 6, . . .} = 1 + 5z
[2] = {. . ., -3, 2, 7, . . .} = 2 + 5z
[3] = {. . ., -2, 3, 8, . . .} = 3 + 5z
. . . . . . . . . . . . . . . . . . . .
[x] = {. . ., -5 + x, x, 5 + x, . . .} = x + 5z

The ring Z/nZ is an algebraic structure with its own arithmetic,
(a + nZ) + (b + nZ) = (a + b) + nZ
(a + nZ) . (b + nZ) = (a . b) + nZ

Example. For Z/5Z, [1] + [2] = [3] and [2].[3] = [6]
[1] + [2] = (1 + 5Z) + (2 + 5Z) = (1 + 2) + 5Z = 3 + 5Z = [3] = {. . ., -2, 3, 8, ...}
[2].[3] = (2 + 5Z) . (3 + 5z) = (2 . 3) + 5z = 6 + 5z = [6] = {. . ., 1, 6, 11, . . .}

Z/nZ is a set of mathematical objects similar to the typical sets of numbers we are all used to dealing with from high school (N, Z, Q, R). The operations are also familiar, given they are the same from the algebra studied in hs (mostly linear equations of the form y = mx + b).

The upshot of these fancy theorems from Abstract Algebra is that the structures that make the algebra you are familiar with are not unique to just the real numbers (numbers you are used to) and can be imposed on other mathematical objects, where Z/nZ is one of those objects.

Quickly we touch upon a function I should have included in the last post.

Greatest Common Divisor
Let gcd(a, b) = max{d in Z: d|a and d|b} unless both a and b are 0 in which case gcd(0, 0) = 0

We could cover a lot of lemmas for gcd but we will not, I'm just saying it too has a lot of intereting arithmetic properties.

The key take away is how it relates to primes and factorization, if p is a prime number and p | abwhere a and b are in Z, then p | a and p | b. It's immediately apparent from this statement and the definition of gcd that prime factorization is a way to solve gcd.

The Group of Units of the Ring Z/nZ
Let (Z/nZ)* be the set of all elements [x] in Z/nZ such that gcd(x,n) = 1.

Notice to be in this Group of Unites the elements x and n must satisfy the condition gcd(x, n) = 1, therefore the only divisor these two elements can share is 1 which is the condition for being 'coprime'.

Example. let x = 8 and n = 9, gcd(8, 9) = 1 and as such 8 and 9 are coprime despite that individually they are not prime numbers.

So all elements in (Z/nZ)* are the coprime elements found in [x] = {a in Z | a ≅ x (mod n)}.

This next definition and its corresponding theorems are the reason all of the above matters.

Eulers φ Function
For n in N, let φ((n) = #{a in N : a <= n and gcd(a,n) = 1}

the function φ(n) outputs the number of elements a with the following two properties,
(1) a <= n which creates a upper bound of what the output of φ((x) can be, it will never be greater than its input.
(2) The numbers a and n must be coprime.

Example.
φ((4) = #[1, 2, 3, 4]
The list of numbers are derived from the the first property, a <= n
Now we must count the coprime numbers with 4, in this case that is 1 and 3
Hence φ((4) = 2

φ((5) = #[1, 2, 3, 4, 5]
Again the list is derived from the property a <= n
We count the coprime numbers with 5, we get 1, 2, 3, 4
Hence φ((5) = 4

Notice that for the case φ((5) n = 5 is a prime number and it was the only number deleted from the list of coprimes. This turns out to be a property that holds generally.

φ((p) = #{1, 2, . . ., p-1} = p-1

Eulers Theorem
If gcd(x, n) = 1, then x^φ((n) ≅ 1 (mod n)

Wilsons Theorem
An integer p > 1 is prime if and only if (p - 1)! ≅ -1 (mod p)

Psuedoprimality
An integer p > 1 is prime if and only if for every a ≅ 0 (mod p), a^(p-1) ≅ 1 (mod p)

From Eulers Theorem and Wilsons Theorem we derive the Pseudoprimatility theorem which is a test fro prime numbers, it effectively connects Z/nZ to the concept of primes computationally by paving away for testing for prime numbers via integer modulo n algebra.

Its important to state that these primality theorems states that a given number is probably prime.These tests are easily programmable, hence many algorithms that test for prime numbers are based on these and therefore the set of tests that are derivable from Eulers Theorem are the foundation for algorithms used in cryptography.

With my idears and your nerd stuff we can do anything !

Cryptography I : Diffie-Hellman

The goal of public key cryptography is to share secrets securely with other parties under the assumption that they will be intercepted by parties we don't want to read them.

Modern cryptography is only possible because of the breakthroughs in Algebraic Number Theory, which I outlined in the last post. Everything we are about to discuss are applications of the mathematical objects Z/nZ and (Z/nZ)*

The first protocol we will explore is the Diffie-Hellman Key exchange because its one of the oldest, its relatively simple, and still in use.

The Diffie-Hellman Protocol,

(1) Alice and Tony choose an integer p that is (probably) a prime number.
(2) Alice and Tony Choose a number g such that 1 < g < p
(3) Alice chooses a number n in Z and keeps it a secret from everyone including Tony
(4) Tony chooses a number m in Z and keeps it a secret from everyone including Alice
(5) Alice computes g^n (mod p) and gives the value to Tony
(6) Tony computes g^m (mod p) and gives the value to Alice
(7) The secret key that has been shared is s ≅ (g^n)^m ≅ (g^m)^n ≅ g^(nm) (mod p)

The protocol is relatively simple and once you get a hang of computing via modular arithmetic finding the values is pretty easy.

Notice the protocol requires the use of Integer Modulo n, or rather that values such as s are elements Z/nZ

In fact p defines what Z/nZ is because n = p so when we chose p we are choosing Z/nZ = Z/pZ

A more implicit fact is that g will belong to (Z/pZ)*, that is p and g are coprime which is to say that gcd(g, p) = 1 (refer back to last post section The Group of Units of Ring Z/nZ)

By choosing p we choose Z/pZ which then dictates (Z/pZ)* from which we derive g.

The secret numbers n and m that Alice and Tony choose but do not share should be large and randomly generated.

Once g, n, and m are know Alice and Tony can derive g^n, g^m, (g^n)^m, (g^m)^n, and g^nm using familiar exponentiation. Of course (g^n)^m = (g^m)^n = g^nm.

All of these exponential values are elements of the set (Z/pZ)*

The value s ≅ (g^n)^m ≅ (g^m)^n ≅ g^(nm) (mod p) is the secret key that allows Alice and Tony to Encrypt and Decrypt their secret messages.

If you have studied Data Structures then Z/nZ should seem less abstract to you given in this protocol Z/nZ is just a data structure. The abstract theorems and definitions from the last post merely determine what kind of operations and algorithms can manipulate and traverse this data structure. The elements in the Z/nZ data structure are determined once we choose p. Of course by this same logic (Z/pZ)* is also a data structure.

Example.

We will choose the prime number 53 to be p

p = 53
gcd(53, 3) = 1
g = 3
n = 8 (randomly generated)
m = 9 (randomly generated)
g^n = 6561
g^m = 19683
g^nm = 22528399544939174411840147874772641
g^nm (mod 53) = 49

All information in the protocol is public except for n and m, even g^n and g^m are public.

Someone attacking the protocol has the goal of finding s, but to do that they need the values of n and m. Knowing g^n and g^m do not explicitly give you n and m, these are functions and the attacker is only seeing the output of the function and not the input which would contain n and m.

To find n and m an attacker uses knowledge of g and g^n and g^m, the best way to do this is using logarithms given they undo exponentiation.

The value the attacker sees is x and he knows that x = g^n, then log_g(x) = n where g is the base of the log function.

The protocol relies on n and m but there is a simple function that can compute n and m using public knowledge of the correspondence between Alice and Tony. How is the protocol secure then?

Its secure because g is not any old number, g is an element of (Z/pZ)* and computing logs with bases in (Z/pZ)* is computationally costly. Its still not impossible to compute n and m this way, it just takes a really long time and so the goal is to choose p and g such that the complexity of computing n and m is massive.

This is an open problem in Cryptography

Discrete Log Problem
Let G be a finite group such that G = (Z/pZ)*. Given g in G and a power x of g, find a positive integer n such that g^n = x.

In HS algebra functions log(x) are common but there bases are real numbers and therefore the functions themselves are continuous as shown below, (ignore the break in the graph around x = 5.5, that should not be there)

When the base g is in (Z/nZ)* the function is discrete and random the graph is more erratic,

Its obvious from the graph why the base in (Z/nZ)* function is more difficult to deal with.

To be clear the example given is not realistic because we are using small values of p, g, n, and m. In actuality we would use an algorithm that tests primality to find a sufficiently large prime number p, and that prime number p needs to have a specific order so that we can compute g in (Z/pZ)*.

The example does convey exactly how the protocol works and its weaknesses, the only thing that makes it unrealisitic is that we would choose our values in a algorithmic way to ensure security.

The criteria for a proper value p is given by the following proposition,

Suppose p is a prime such that (p-1)/2 is also prime. Then each element of (Z/pZ)* has order one of 1, 2, (p-1)/2, or p-1.

Of course for p = 53, (p-1)/2 = 26 which is not prime, therefore the elements in (Z/pZ)* will not have the orders we want to ensure security.

I liked the part that goes...

AliceInWonderland said:

The protocol relies on n and m but we just that there is a simple function that can compute n and m using public knowledge of the correspondence between Alice and Tony. How is the protocol secure then?

Its secure because g is not any old number, g is an element of (Z/pZ)* and computing logs with bases in (Z/pZ)* is computationally costly. Its still not impossible to compute n and m this way, it just takes a really long time and so the goal is to choose p and g such that the complexity of computing n and m is massive.

 

 Can be cracked by a super computer, but then, in practice the Bitcoin blockchain is a super computer, biggest in the world, which is too rass to crack.

Quantum computing might destroy the security of blockchain, though I don't think they'll just hand them out if they could produce them so easily.

 Fixed the grammatical retardation, thank you for pointing it out implicitly.

Admirer said: 

I liked the part that goes...

AliceInWonderland said:

The protocol relies on n and m but we just that there is a simple function that can compute n and m using public knowledge of the correspondence between Alice and Tony. How is the protocol secure then?

Its secure because g is not any old number, g is an element of (Z/pZ)* and computing logs with bases in (Z/pZ)* is computationally costly. Its still not impossible to compute n and m this way, it just takes a really long time and so the goal is to choose p and g such that the complexity of computing n and m is massive.

 

 Can be cracked by a super computer, but then, in practice the Bitcoin blockchain is a super computer, biggest in the world, which is too rass to crack.

Quantum computing might destroy the security of blockchain, though I don't think they'll just hand them out if they could produce them so easily.

Yes, and for integer modulo prime which is the form I have outlined above the record for cracking discrete log problem is for primes of 256 bits.

The following link provides more information on records for cracking discrete log problem for different forms: Discrete Log Records

That seems like a fun area of research.

Just in case I'll mention I don't notice errors, I just understand.

I did understand the whole thing granted you've assigned meanings to the letters. It does however take quite a bit of time to digest. I mean I see it happening though not sure why.

Elliptic Curves and Geometric Structures

Now its time to talk about Elliptic Curves abstractly, this is the final abstract topic before touching upon Elliptic Curve Cryptography and finally the protocols that make cryptocurrency work.

What makes Elliptic Curves so useful in Number Theory and Cryptography is that we can associate Finite Abelian Groups to these curves and Integer Modulo n, that is Z/nZ is a finite abelian group.

Elliptic Curve
An alliptic curve over a field K is a curve defined by an equation y^2 = x^3 + ax + b where a,b are in K and -16(4a^3 + 27b^2) =/= 0

By definition elliptic curves are just 3rd degree polynomials which should be familiar if you've take precalc or calc.

What sets this 3rd degree polynomial apart from the ones experienced in HS is that its coefficients a and b are not necessarily real numbers in R but rather some numbers that satisfy the field axioms.

The additional condition -16(4a^3 + 27b^2) =/= 0 is to mean that the curve must be "non-singular".

For a curve to be nonsingular it cannot intersect itself or have cusps.

When we construct an elliptic curve we do so over a specified set of numbers that satisfy the field axioms, that is typically over the set Q (rational), R (real), or C (complex).

Below you see an Elliptic Curve y^2 = x^3 - 5x + 4 over the set of Real Numbers,

The above curve is an elliptic because it satisfies the definition, its a third degree polynomial whose numbers a, b are in a filed K (specifically R), and its points are nonsingular.

The group Z/nZ is also a finite field, hence we can define an elliptic curve over this set of number objects.

Below you see an elliptic curve y^2 = x^3 + x over the finite field Z/37Z,

We are particularly interested in Elliptic Curves with Abelian Group Structures.

Let the set E(K) exist such that E(K) = {(x,y) in KxK: y^2 = x^3 + ax + b} U {ס}

The set E(K) contains K-rational points on some elliptic curve E that is over a field K.

The set of points that define the curve is in union with a set {ס} which is a point on the curve E at infinity.

It is on this set E(K) that we want to impose a abelian group structure, we do so by declaring the following algorithm.

Elliptic Curve Group Law
Given P_1, P_2 in E(K), this algorithm computes a third point R = P_1 + P_2 in E(K).
(1) If P_1 = ס set R = P_2 or if P_2 = ס set R = P_1 and terminate. Otherwise write (x_i,y_i) = P_i
(2) If x_1 = x_2 and y_1 = -y_2, set R = ס and terminate
(3) Set λ = {(a) (3x_1^2 + a)/(2Y-1) if P_1 = P_2, (b) (y_1 - y_2)/(x_1 - x_2) otherwise}
(4) Then R = (λ^2 - x_1 - x_2, -λx_3 - v), where c = y_1 - λx_1 and x_3 = λ^2 - x_1 - x_2 is the x coordinate of R.

The algebraic importance of this algorithm is that it defines the operation (+) in respect to the set E(K), and by doing so if imposes a abelian group structure on that set.

More intuitively, the algorithm gives us the ability to define points P_1 and P_2 and the operation (+) to find a third point on the curve.

These points are special because they have a specific geometric relationship with the curve they sit on and that relationship has wide ranging applications in pure and applied mathematics.

Geometric Group Law
Suppose P_i = (X_i,y_i), i = 1, 2 are distinct points on an elliptic curve y^2 = x^3 + ax + b, and that x_1 =/= x_2. Let L be the unique line through P_1 and P_2. Then L intersects the curve E at exactly one other point Q = (λ^2 - x_1 - x_2, λx_3 + c) where λ=(y_1 - y_2)/(x_1 - x_2) and v = y_1 - λx_1

In the following example you see a visual of what's been described above,

The group laws hold for any set set of points P_1, P_2, and P_3 that we choose on any elliptic curve over K, that makes this group structure and incredibly useful to us because it effectively defines a object for which we can do arithmetic over.

This sets us up for using Elliptic Curves to do things like Prime Factorization.

Power Smooth
Let B be a positive integer. If n is a positive integer with prime factorization n = ∏p_i^e_i then n is a B-Power Smooth if p_i^e_i <= B for all i

This sounds a bit weird if not familiar with the symbols, so lets just do an example

Example.
30 = 2*3*5 therefore 30 is a B-Power Smooth of 5
150 = 2*3*5^2 = 2*3*25 therefore 150 is a B power smooth of 25

Just treat the largest prime factor as the B power smooth.

The B Power Smooth allows us to declare the following algorithm,

Least Common Multiple of First B Integers
(1) Compute a list P of all primes p <= B
(2) Compute and outpute the product ∏p^[log_p(B)]

The algorithm above, denoted via the function lcm() usually, allows us to compute the least common multiple of positive integers up to B.

The reason we need the two previous results is that they allow us to declare an algorithm that uses elliptic curves in integer factorization,

Elliptic Curve Factorization Method
(1) Compute lcm() using Least Common Multiple of First B Integers Method
(2) Choose a random Elliptic Curve
(3) Compute mP using curve.

For step (2) we choose some number a in Z/nZ such that 4a^3 + 27 is in (Z/nZ)*, in doing so we know that P = (0,1) will be a point on the elliptic curve over Z/nZ.

Given we get to choose any curve E over Z/nZ we are not restricted by the groups E(Z/nZ) we can choose.

Cryptography II: Elliptic Curve Cryptography

Elliptic Curve cryptography does not necessarily a replacement for other forms of cryptography from the standpoint of being more secure than them. We've seen when reviewing the Discrete-Log problem even simple protocol such as the Diffie-Hellmen that past a certain key size the protocols are really secure (unless an unknown backdoor exists).

The problem many cryptographic systems face is that to assure security their key sizes need to be quite large. The actual benefit of Elliptic curve cryptography is that it requires smaller key sizes while assuring the same level of security.

An analog of Diffie-Hellman exists for Elliptic Curves. The protocol is very similar, the major difference is that the mathematical object of interest from which we derive values is an Elliptic Curve as opposed to (Z/pZ)*

As an example of a EEC system we will use ElGamal protocol.

ElGamal System
(1) Alice chooses a prime number p (using algorithms previous described)
(2) Alice chooses an elliptic curve defined over Z/pZ, E(Z/pZ)
(3) Alice chooses a point B in E(Z/pZ)
(3) Alice chooses a random integer n that she keeps secret from everyone
(4) Alice shares publicly p, E, B, and nB

The public key Alice shares is (p, E, B, nB).

If Tony wants to communicate with Alice via this system,
(1) Tony encodes a message as an element P in E(Z/pZ)
(2) Tony computes a random integer r
(3) Tony computes the points rB and P + r(nB) in E(Z/pZ)

Tony has now encrypted his message P as the key pair (rB, P+r(nB))

If Alice wants to decrypt Tonys message,
(1) Alice multiplies rB by her secret key n to obtain n(rB) = r(nB)
(2) Alice subtracts n(rB) from P + r(nb) to obtain P

Again, the success of this protocol is owed to the secret keys n and r which no one knows but Alice and Bob respectively.

An example, 

p = 785963102379428822376694789446897396207498568951

Hence, we have the curve E(Z/785963102379428822376694789446897396207498568951Z) ,   

y^2 = x^3 + 317689081251325503476317476413827693272746955927*x + 79052896607878758718120572025718535432100651934

Let the point in E(Z/pZ) be,

B = (771507216262649826170648268565579889907769254176 : 390157510246556628525279459266514995562533196655 : 1)

we randomly generate two integers in Z/nZ, one being Alices secret number n and the other Tonys secret number r 

n=670805031139910513517527207693060456300217054473

r=70674630913457179596452846564371866229568459543

The secret message Tony has created, 

P = (14489646124220757767 : 669337780373284096274895136618194604469696830074 : 1)

Alice and Tony share their public keys n*B and r*B respectively, 

n*B = (144686662901404309225022255991457337359579312971 : 783422538889314742320028661515570074788056556263 : 1)

r*B = (746969216401233383489928979051523943667260169795 : 33490393191968417904944324593414645179583458780 : 1)

Tony encrypts his message P and shares the key pair,

[r*B, P + r*(n*B)] = 

[(746969216401233383489928979051523943667260169795 : 33490393191968417904944324593414645179583458780 : 1),
(396559123489688031896418653419157280824050893098 : 213777225982147522115309257148514559653140828398 : 1)]

The encrypted secret message is, 

P + r*(n*B)  = 396559123489688031896418653419157280824050893098 : 213777225982147522115309257148514559653140828398 : 1)

To decrypt Tonys message Alice needs the value of r*(n*B) which is, 

r*(n*B) = (580760036773191537360137853276477173103700091567 : 484341509975162967079842153001139824341683545703 : 1)

However, r*(n*B) = n(*r*B) because multiplicative associativity,

n*(r*b)  = (580760036773191537360137853276477173103700091567 : 484341509975162967079842153001139824341683545703 : 1)

Alice computes,

P + r*(n*B) - n*(r*B) = 

(14489646124220757767 : 669337780373284096274895136618194604469696830074 : 1)

Hence P = P + r*(n*B) - n*(r*B) and Alice has the message P